Consistent tools for graph analysis#

NNGT provides several functions for topological analysis that return consistent results for all backends (the results will always be the same regardless of which library is used under the hood). This section describes these functions and gives an overview of the currently supported methods.

Note

It is of course possible to use any function from the library on the graph attribute; however, not using one of the supported NNGT functions below will usually return results that are not consistent between libraries (and the code will obviously no longer be portable).

Supported functions#

The following table details which functions are supported for directed and undirected networks, and whether they also work with weighted edges.

The test file where these functions are checked can be found here: testing/library_compatibility.py.

For each type of graph, the table tells which libraries are supported for the given function (graph-tool is gt, networkx is nx and igraph is ig). Custom implementation of a function is denoted by nngt, meaning that the function can be used even if no graph library is installed. A library marked between parentheses denotes partial support and additional explanation is usually given in the footnotes. A cross means that no consistent implementation is currently provided and the function will raise an error if one tries to use it on such graphs. Methods that are not defined for weighted or directed graphs are marked by NA.

Method	Unweighted undirected	Unweighted directed	Weighted undirected	Weighted directed
`all_shortest_paths()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`average_path_length()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`assortativity()` [1]	gt, nx, ig	gt, nx, ig	gt, ig	gt, ig
`betweenness()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`betweenness_distrib()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`closeness()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`connected_components()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`degree_distrib()`	gt, nx, ig, nngt	gt, nx, ig, nngt	gt, nx, ig, nngt	gt, nx, ig, nngt
`diameter()` [2]	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`global_clustering()`	gt, nx, ig, nngt	nngt	nngt	nngt
`local_clustering()` [3]	gt, nx, ig, nngt	nngt	nngt	nngt
`reciprocity()`	gt, nx, ig, nngt	gt, nx, ig, nngt	NA	NA
`shortest_distance()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`shortest_path()`	gt, nx, ig	gt, nx, ig	gt, nx, ig	gt, nx, ig
`spectral_radius()`	nngt	nngt	nngt	nngt
`subgraph_centrality()`	nngt	nngt	nngt	nngt
`transitivity()` [4]	gt, nx, ig, nngt	nngt	nngt	nngt

Clustering in weighted and directed networks#

For directed clustering, NNGT provides the total clustering proposed in [Fagiolo2007]

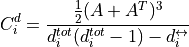
$C_i^d = \frac{\frac{1}{2} (A + A^T)^3}{d_i^{tot}(d_i^{tot} - 1) - d_i^{\leftrightarrow}}$

with 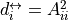$d_i^{\leftrightarrow} = A^2_{ii}$ is the reciprocal degree.

For undirected weighted clustering, NNGT provides the definition proposed in [Barrat2004], [Onnela2005], [Zhang2005] as well as a new continuous definition [Fardet2021].

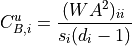
$C_{B,i}^u = \frac{(WA^2)_{ii}}{s_i (d_i - 1)}$

$C_{O,i}^u = \frac{(W^{\left[\frac{1}{3}\right]})^3_{ii}}{d_i (d_i - 1)}$

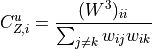
$C_{Z,i}^u = \frac{(W^3)_{ii}}{\sum_{j \neq k} w_{ij} w_{ik}}$

$C_{c,i}^u = \frac{\left(W^{\left[\frac{2}{3}\right]}\right)^3_{ii}}{\left(s^{\left[\frac{1}{2}\right]}_i\right)^2 - s_i}$

with $s^{\left[\frac{1}{2}\right]}$ the generalized strength associated to the matrix $W^{\left[\frac{1}{2}\right]} = \{\sqrt{w_{ij}}\}$ .

For directed weighted clustering, the generalization of Barrat from [Clemente2018] is provided, as well as a generalization of Onnela, Zhang–Horvath, and of the continuous clustering [Fardet2020], for all four directed modes (middleman, cycle, fan-in, and fan-out), as well as their sum, the total clustering:

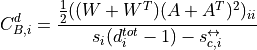
$C_{B,i}^d = \frac{\frac{1}{2}((W + W^T)(A+A^T)^2)_{ii}}{s_i (d_i^{tot} - 1) - s_{c,i}^{\leftrightarrow}}$

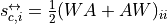with $s$ the total strength and $s_{c,i}^{\leftrightarrow} = \frac{1}{2} (WA + AW)_{ii}$ the arithmetic reciprocal strength,

$C_{O,i}^d = \frac{\frac{1}{2}(W^{\left[\frac{1}{3}\right]} + (W^{\left[\frac{1}{3}\right]})^T)^3_{ii}}{d_i^{tot}(d_i^{tot} - 1) - d_i^{\leftrightarrow}}$

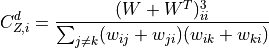
$C_{Z,i}^d = \frac{(W + W^T)^3_{ii}}{\sum_{j \neq k} (w_{ij} + w_{ji})(w_{ik} + w_{ki})}$

$C_{c,i}^d = \frac{\frac{1}{2}\left(W^{\left[\frac{2}{3}\right]} + W^{\left[\frac{2}{3}\right],T}\right)^3_{ii}}{\left(s^{\left[\frac{1}{2}\right]}_i\right)^2 - 2s^{\leftrightarrow}_i - s_i}$

with $s^{\left[\frac{1}{2}\right]}$ the total generalized strength and $s_i^\leftrightarrow = \left( W^{\left[\frac{1}{2}\right]} \right)^2$ the geometric reciprocal strength.

Global clusterings are defined as the sum of all numerators divided by the sum of all denominators for all definitions.

References#

[Barrat2004]

Barrat, Barthelemy, Pastor-Satorras, Vespignani. The Architecture of Complex Weighted Networks. PNAS 2004, 101 (11). DOI: 10.1073/pnas.0400087101.

[Clemente2018]

Clemente, Grassi. Directed Clustering in Weighted Networks: A New Perspective. Chaos, Solitons & Fractals 2018, 107, 26–38. DOI: 10.1016/j.chaos.2017.12.007, arXiv: 1706.07322.

[Fagiolo2007]

Fagiolo. Clustering in Complex Directed Networks. Phys. Rev. E 2007, 76, (2), 026107. DOI: 10.1103/PhysRevE.76.026107, arXiv: physics/0612169.

[Onnela2005]

Onnela, Saramäki, Kertész, Kaski. Intensity and Coherence of Motifs in Weighted Complex Networks. Phys. Rev. E 2005, 71 (6), 065103. DOI: 10.1103/physreve.71.065103, arXiv: cond-mat/0408629.

[Saramaki2007]

Saramäki, Kivelä, Onnela, Kaski, Kertész. Generalizations of the Clustering Coefficient to Weighted Complex Networks. Phys. Rev. E 2007, 75 (2), 027105. DOI: 10.1103/PhysRevE.75.027105, arXiv: cond-mat/0608670.

[Zhang2005]

Zhang, Horvath. A General Framework for Weighted Gene Co-Expression Network Analysis. Statistical Applications in Genetics and Molecular Biology 2005, 4 (1). DOI: 10.2202/1544-6115.1128, PDF.

[Fardet2021]

Fardet, Levina. Weighted directed clustering: interpretations and requirements for heterogeneous, inferred, and measured networks. 2021. arXiv: 2105.06318.

Go to other tutorials: